SAR data contains Amplitude Α and Phase Ø. Amplitude is the backscatter which depends on surface roughness and dielectric constant of the scatters. In Interferometric SAR (InSAR) we are work with phase variation.  Phase is the fraction of  a fully sinusoidal wave cycle which is related to the distance travelled by the signal to and from the target. The phase value at a particular pixel Ø(P) is a function of many contributions. The dominant phase combination within a pixel is defined by 4π/λR. There is also φ which is the phase contribution from many scatterers within a pixel. In addition. there is phase contribution from atmospheric delay α as well as from the noise source (v).

So the total phase from a pixel is:

Ø(P) = 4π/λR + φ + α + v     (1)

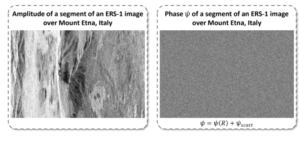Figure 1  shows SAR image backscatter (left) and Phase (right). Unlike the backscatter of SAR image, phase value of a single SAR image does not provide any useful information. Information can only be derived by comparing phase values of two SAR images. This is done by calculating the difference of the phase values at similar pixel P between two SAR images. The condition that pixel should be same on the two images emphasizes on the significance of image co-registration in InSAR. The phase difference then becomes:’

ΔØ(P) = 4π/λΔR + Δφ + Δα + Δv (2)

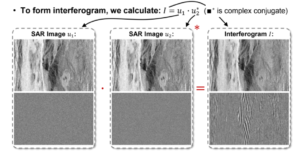
The resulting phase difference of the all pixels of two SAR images is the interferogram, I (see figure beside). Technically, this is done by multiplying the the complex values of the first SAR image (called master image) with the complex conjugate of the second SAR image (slave image); I = U1.U2* (see illustration below)

If we assume that the two SAR images have uniform scatterers, acquired at the same atmospheric condition and there is no or negligible noise contribution, then equation 2 reduces to:

ΔØ(P) = 4π/λΔR   (3)

This relation contains a term ΔR which is a measure of the range variation between the two SAR images.  Such a system that can measure range variation can be used to estimate elevation.  The perception of depth by our eyes and brain has a similar working principle. If the SAR images of the same area is observed from exactly same location at different times, the range variation can also also be used to determine deformation over the period.

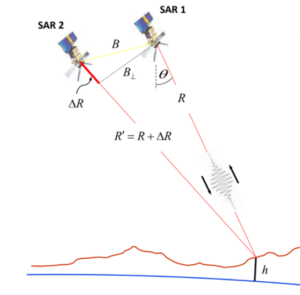In principle, InSAR requires that we acquire at least two SAR images of the same location. The two images have to be acquired from different position or at different time. If the images are acquired simultaneously (same time) at different location (non-zero baseline), there will be no earth movement component and atmospheric disturbance as they affect the two acquisitions equally and cancel out. This method is called Single-Pass Interferometry and it is usually employed in generating DEM from SRTM or TanDEM-X. If the images are acquired at multiple times, this method is called repeat-pass interferometry and this technique can be used to monitor the deformation between the acquisition period.