This notebook is a practical demonstration of an exploratory data analysis task. For this task, we want to understand how completion rates differ for different types of students and different types of schools. We want to look at this by:
- Student race
- Admission policy and rate
- Public/private status (the documentation describes this as “control” — what is the legal or financial control status of the school?)
We will work with the data set underlying the Department of Education’s College Scorecard. This is a medium-sized data set. We will only work with the most recent cohort’s data.
Motivation.¶
The data was created to promote openness by giving students and families the ability to assess different colleges are preparing performing and preparing its students for the workforce. The public, particularly students and families can use the data to compare the costs and results of various universities.
The instituition data is part of the large College Scoredcard project of the U.S Department of Education. The data is collected annually through surveys administered by the Department of Education’s National Center for Education Statistics (NCES), IPEDS is the primary source of data on postsecondary education institutions in the United States.
Composition¶
There are about 10 instances in the data:
- Academics : This instance describes the types of academic offerings available at each institution.
- Admissions : This instance This information describes the admissions rate and SAT/ACT scores of students aids.
- Aid : This instance covers information on financial aid including Pell Grants and federal student loans which help many students particularly low-incone students access and afford a higher education.
- Completion : This instance contains information on college completion which determines other positive outcones such as finding a job and succesfully repaying student loans.
- Cost : This instance contains information about the costs to students of an institution which can provide important context for students and families as they seek to evaluate the tradeoffs of access, affordability, and outcomes.
- Earnings : This instance contains information on the earnings and employment prospects of former students.
- Repayment : This instance provides information on the debt burden of attending college and the loan performance metrics for each institution.
- School : This instance provides basic descriptive information about the institution in question. These include: identifiers, location, degree type and profile, programs offered, and the academic profile of students enrolled.
- Student : This instance identifies demographic and other details about the student body of the institution. The category under this include number of undergraduate students, student body by race, gender, age, Part-Time/Full-Time status, family income
Q4: Does the dataset identify any subpopulations (e.g., by age, gender)? If so, please describe how these subpopulations are identified and
provide a description of their respective distributions within the dataset.
Yes. The instituitional data contains several elements that identify demographic based on their age, sex and race. The race and gender are reported by the instituitions to IPEDS in the fall enrollment components and rely on student’s self-reported race and gender data as collected by the instituition.
#import packages
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
0. Data Cleaning¶
read the data¶
# read the csv file
schools = pd.read_csv('../../Data/Most-Recent-Cohorts-Institution_04262022/Most-Recent-Cohorts-Institution.csv',
usecols= ['INSTNM', 'CITY', 'STABBR', 'ST_FIPS', 'CONTROL', 'HIGHDEG', 'ICLEVEL', 'C150_4', 'C150_4_POOLED', 'C150_L4', 'C150_L4_POOLED', 'C100_4', 'C100_4_POOLED', 'C100_L4', 'C100_L4_POOLED',
'OPENADMP', 'ADM_RATE', 'ADM_RATE_ALL'])
#create a dictionary variable to use for encoding ST_FIPS column
state_name = {1: 'Alabama', 2 : 'Alaska', 4 : 'Arizona', 5 : 'Arkansas', 6 : 'California', 8 : 'Colorado', 9 : 'Connecticut', 10 : 'Delaware',
11 : 'District of Columbia', 12 : 'Florida', 13 : 'Georgia', 15 : 'Hawaii', 16 : 'Idaho', 17 : 'Illinois', 18 : 'Indiana', 19 : 'Iowa', 20 : 'Kansas',
21: 'Kentucky', 22 : 'Louisiana', 23 : 'Maine', 24 : 'Maryland', 25 : 'Massachusetts', 26 : 'Michigan', 27 : 'Minnesota', 28 : 'Mississippi', 29 : 'Missouri', 30 : 'Montana',
31 : 'Nebraska', 32 : 'Nevada', 33 : 'New Hampshire', 34 : 'New Jersey', 35 : 'New Mexico', 36 : 'New York', 37 : 'North Carolina', 38 : 'North Dakota', 39: 'Ohio', 40 : 'Oklahoma',
41 : 'Oregon', 42 : 'Pennsylvania', 44 : 'Rhode Island', 45 : 'South Carolina', 46 : 'South Dakota', 47 : 'Tennessee', 48 : 'Texas', 49 : 'Utah', 50 : 'Vermont',
51 : 'Virginia', 53 : 'Washington', 54 : 'West Virginia', 55 : 'Wisconsin', 56 : 'Wyoming', 60 : 'American Samoa', 64 : 'Federated States of Micronesia', 66 : 'Guam',
69 : 'Northern Mariana Islands', 70 : 'Palau', 72 : 'Puerto Rico', 78 : 'Virgin Islands'}
# encode ST_FIPS to the state name and drop the column
schools['STATE'] = schools.ST_FIPS.map(state_name)
schools = schools.drop(['ST_FIPS'], axis = 1)
# create a dictionary variable to use for encoding CONTROL
control_name = {1 : 'Public', 2 : 'Private, Nonprofit', 3 : 'Proprietary'}
# encode CONTROL column and drop the column
schools['CONTROL_STATUS'] = schools.CONTROL.map(control_name)
schools = schools.drop(['CONTROL'], axis = 1)
# create a dictionary to use for encoding Highest award column
highdegree_name = {0 : 'Non-degree-granting', 1: 'Certificate degree', 2 : 'Associate degree', 3 : 'Bachelor degree' , 4 : 'Graduate degree'}
# encode HIGHDEG column and drop the column
schools['HIGHDEG_TYPE'] = schools.HIGHDEG.map(highdegree_name)
schools = schools.drop(['HIGHDEG'], axis = 1)
# create a dictionary to use for encoding Level of Instituition
iclevel_name = {1 : '4 Year', 2 : '2 Year', 3 : 'Less than 2 year'}
# encode ICLEVEL column and dropm the column
schools['ICLEVEL_TYPE'] = schools.ICLEVEL.map(iclevel_name)
schools = schools.drop(['ICLEVEL'], axis= 1)
schools
| INSTNM | CITY | STABBR | ADM_RATE | ADM_RATE_ALL | C150_4 | C150_L4 | C150_4_POOLED | C150_L4_POOLED | C100_4 | C100_L4 | OPENADMP | C100_4_POOLED | C100_L4_POOLED | STATE | CONTROL_STATUS | HIGHDEG_TYPE | ICLEVEL_TYPE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Alabama A & M University | Normal | AL | 0.8965 | 0.8965 | 0.2866 | NaN | 0.2918 | NaN | 0.1052 | NaN | 2.0 | 0.0929 | NaN | Alabama | Public | Graduate degree | 4 Year |
| 1 | University of Alabama at Birmingham | Birmingham | AL | 0.8060 | 0.8060 | 0.6117 | NaN | 0.6229 | NaN | 0.3816 | NaN | 2.0 | 0.3920 | NaN | Alabama | Public | Graduate degree | 4 Year |
| 2 | Amridge University | Montgomery | AL | NaN | NaN | 0.2500 | NaN | 0.2857 | NaN | 0.2500 | NaN | 1.0 | 0.2400 | NaN | Alabama | Private, Nonprofit | Graduate degree | 4 Year |
| 3 | University of Alabama in Huntsville | Huntsville | AL | 0.7711 | 0.7711 | 0.5714 | NaN | 0.5740 | NaN | 0.3109 | NaN | 2.0 | 0.2914 | NaN | Alabama | Public | Graduate degree | 4 Year |
| 4 | Alabama State University | Montgomery | AL | 0.9888 | 0.9888 | 0.3177 | NaN | 0.3235 | NaN | 0.1462 | NaN | 2.0 | 0.1571 | NaN | Alabama | Public | Graduate degree | 4 Year |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 6657 | Pennsylvania State University-Penn State Wilke… | Lehman | PA | NaN | 0.7827 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year |
| 6658 | Pennsylvania State University-Penn State York | York | PA | NaN | 0.7827 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year |
| 6659 | Pennsylvania State University-Penn State Great… | Malvern | PA | NaN | 0.7827 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year |
| 6660 | Pennsylvania State University-Penn State Harri… | Middletown | PA | NaN | 0.7827 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year |
| 6661 | Pennsylvania State University-Penn State Brand… | Media | PA | NaN | 0.7827 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year |
6662 rows × 18 columns
# check the data structure
schools.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 6662 entries, 0 to 6661 Data columns (total 18 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 INSTNM 6662 non-null object 1 CITY 6662 non-null object 2 STABBR 6662 non-null object 3 ADM_RATE 1960 non-null float64 4 ADM_RATE_ALL 2234 non-null float64 5 C150_4 2270 non-null float64 6 C150_L4 3180 non-null float64 7 C150_4_POOLED 2292 non-null float64 8 C150_L4_POOLED 3207 non-null float64 9 C100_4 2007 non-null float64 10 C100_L4 3180 non-null float64 11 OPENADMP 5691 non-null float64 12 C100_4_POOLED 2046 non-null float64 13 C100_L4_POOLED 3207 non-null float64 14 STATE 6661 non-null object 15 CONTROL_STATUS 6662 non-null object 16 HIGHDEG_TYPE 6662 non-null object 17 ICLEVEL_TYPE 6662 non-null object dtypes: float64(11), object(7) memory usage: 937.0+ KB
Fill in the missing values¶
There are lot of missing values in the completion rate columns as shown by the info above. There are about 6662 records of instuitions in the database but the completion rate variables have way less. For example, C150_4 has 2270 non-null values while C150_L4 has about 3180. A way to fill the missing values is to combine these columns if there are no schools in both categories.
#find out if there is any school in both 4 years and less than 4 years column
print(len(schools[schools['C100_4'] == schools['C100_L4']]))
print(len(schools[schools['C150_4'] == schools['C150_L4']]))
0 0
#Filling the 4 years column with less than 4 years column
schools['C_100'] = schools['C100_4'].combine_first(schools['C100_L4'])
schools['C_100_POOLED'] = schools['C100_4_POOLED'].combine_first(schools['C100_L4_POOLED'])
schools['C_150'] = schools['C150_4'].combine_first(schools['C150_L4'])
schools['C_150_POOLED'] = schools['C150_4_POOLED'].combine_first(schools['C150_L4_POOLED'])
#drop the other completion rate columns after filling
schools = schools.drop(['C100_4', 'C100_L4', 'C100_4_POOLED', 'C100_L4_POOLED', 'C150_4', 'C150_L4', 'C150_4_POOLED', 'C150_L4_POOLED'], axis = 1)
schools.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 6662 entries, 0 to 6661 Data columns (total 14 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 INSTNM 6662 non-null object 1 CITY 6662 non-null object 2 STABBR 6662 non-null object 3 ADM_RATE 1960 non-null float64 4 ADM_RATE_ALL 2234 non-null float64 5 OPENADMP 5691 non-null float64 6 STATE 6661 non-null object 7 CONTROL_STATUS 6662 non-null object 8 HIGHDEG_TYPE 6662 non-null object 9 ICLEVEL_TYPE 6662 non-null object 10 C_100 5187 non-null float64 11 C_100_POOLED 5253 non-null float64 12 C_150 5450 non-null float64 13 C_150_POOLED 5499 non-null float64 dtypes: float64(7), object(7) memory usage: 728.8+ KB
Selecting Variables¶
The completion rates for full-time, first-time students who complete within 100 or 150 percent of the expected time to completion are represented by C_100 and C_150 variables respectively. However, only the 150 percent rates are available disaggregated by race. So C_150 would make the most of sense in the context of this task. C_100_POOLED and C_150_POOLED variables are pooled completion rates across two years rolling basis. For self-consistent analysis, I use the normal completion rate variables and not the pooled varaibles.
#drop the POOLED completion rates
schools = schools.drop(['C_100_POOLED', 'C_150_POOLED'], axis = 1)
schools.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 6662 entries, 0 to 6661 Data columns (total 12 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 INSTNM 6662 non-null object 1 CITY 6662 non-null object 2 STABBR 6662 non-null object 3 ADM_RATE 1960 non-null float64 4 ADM_RATE_ALL 2234 non-null float64 5 OPENADMP 5691 non-null float64 6 STATE 6661 non-null object 7 CONTROL_STATUS 6662 non-null object 8 HIGHDEG_TYPE 6662 non-null object 9 ICLEVEL_TYPE 6662 non-null object 10 C_100 5187 non-null float64 11 C_150 5450 non-null float64 dtypes: float64(5), object(7) memory usage: 624.7+ KB
ADMISSIONS¶
There are two variables that describe the admissions practices. OPENADMP indicates whether it has an open admissions policy. 1 -Yes, 2 – No, 3 – Does not enrol first-time student. Second, schools that do not have an open admissions policy (2) report the admission rate. For institutions with multiple branches,
ADM_RATE includes the admissions rate at each campus, while ADM_RATE_ALL represents the admissions rate across all campuses.
We’re going to bucketize the admissions policy. I defined three categories of schools:
- Open-admission schools
- Low-selectivity schools, where the admission rate is higher than the median admission rate
- High-selectivity schools, where the admission rate is lower than the median admission rate
# calculate the median admission rate for ADM_RATE and ADM_RATE_ALL
adm_median = schools['ADM_RATE'].median()
adm_median_all = schools['ADM_RATE_ALL'].median()
print(adm_median)
print(adm_median_all)
0.7518 0.7596499999999999
#Convert admission rate to categorical values
# Bucketize the ADM_RATE variable
schools['ADM'] = 'Open-admission'
schools.loc[schools['ADM_RATE'] < adm_median, 'ADM'] = 'High-selectivity'
schools.loc[schools['ADM_RATE'] > adm_median, 'ADM'] = 'Low-selectivity'
#Bucketize the ADM_RATE_ALL variable
schools['ADM_ALL'] = 'Open-admission'
schools.loc[schools['ADM_RATE_ALL'] < adm_median_all, 'ADM_ALL'] = 'High-selectivity'
schools.loc[schools['ADM_RATE_ALL'] > adm_median_all, 'ADM_ALL'] = 'Low-selectivity'
schools
| INSTNM | CITY | STABBR | ADM_RATE | ADM_RATE_ALL | OPENADMP | STATE | CONTROL_STATUS | HIGHDEG_TYPE | ICLEVEL_TYPE | C_100 | C_150 | ADM | ADM_ALL | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Alabama A & M University | Normal | AL | 0.8965 | 0.8965 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.1052 | 0.2866 | Low-selectivity | Low-selectivity |
| 1 | University of Alabama at Birmingham | Birmingham | AL | 0.8060 | 0.8060 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.3816 | 0.6117 | Low-selectivity | Low-selectivity |
| 2 | Amridge University | Montgomery | AL | NaN | NaN | 1.0 | Alabama | Private, Nonprofit | Graduate degree | 4 Year | 0.2500 | 0.2500 | Open-admission | Open-admission |
| 3 | University of Alabama in Huntsville | Huntsville | AL | 0.7711 | 0.7711 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.3109 | 0.5714 | Low-selectivity | Low-selectivity |
| 4 | Alabama State University | Montgomery | AL | 0.9888 | 0.9888 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.1462 | 0.3177 | Low-selectivity | Low-selectivity |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 6657 | Pennsylvania State University-Penn State Wilke… | Lehman | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6658 | Pennsylvania State University-Penn State York | York | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6659 | Pennsylvania State University-Penn State Great… | Malvern | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6660 | Pennsylvania State University-Penn State Harri… | Middletown | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6661 | Pennsylvania State University-Penn State Brand… | Media | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
6662 rows × 14 columns
TASK REQUIREMENT¶
1. A basic structural description of the data set:¶
- How many schools and variables?
- How many schools are there per state?
- How are schools-per-state distributed? Compute a state-level variable ‘# of schools’, and describe its distribution numerically and visually.
schools
| INSTNM | CITY | STABBR | ADM_RATE | ADM_RATE_ALL | OPENADMP | STATE | CONTROL_STATUS | HIGHDEG_TYPE | ICLEVEL_TYPE | C_100 | C_150 | ADM | ADM_ALL | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Alabama A & M University | Normal | AL | 0.8965 | 0.8965 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.1052 | 0.2866 | Low-selectivity | Low-selectivity |
| 1 | University of Alabama at Birmingham | Birmingham | AL | 0.8060 | 0.8060 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.3816 | 0.6117 | Low-selectivity | Low-selectivity |
| 2 | Amridge University | Montgomery | AL | NaN | NaN | 1.0 | Alabama | Private, Nonprofit | Graduate degree | 4 Year | 0.2500 | 0.2500 | Open-admission | Open-admission |
| 3 | University of Alabama in Huntsville | Huntsville | AL | 0.7711 | 0.7711 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.3109 | 0.5714 | Low-selectivity | Low-selectivity |
| 4 | Alabama State University | Montgomery | AL | 0.9888 | 0.9888 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.1462 | 0.3177 | Low-selectivity | Low-selectivity |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 6657 | Pennsylvania State University-Penn State Wilke… | Lehman | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6658 | Pennsylvania State University-Penn State York | York | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6659 | Pennsylvania State University-Penn State Great… | Malvern | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6660 | Pennsylvania State University-Penn State Harri… | Middletown | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6661 | Pennsylvania State University-Penn State Brand… | Media | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
6662 rows × 14 columns
schools['INSTNM'].nunique()
6530
There are about 6530 schools
schools.groupby('STATE')['INSTNM'].count()
STATE Alabama 87 Alaska 9 American Samoa 1 Arizona 120 Arkansas 90 California 705 Colorado 94 Connecticut 78 Delaware 19 District of Columbia 26 Federated States of Micronesia 1 Florida 394 Georgia 174 Guam 3 Hawaii 23 Idaho 39 Illinois 253 Indiana 136 Iowa 77 Kansas 79 Kentucky 89 Louisiana 121 Maine 37 Maryland 84 Massachusetts 153 Michigan 187 Minnesota 112 Mississippi 59 Missouri 157 Montana 32 Nebraska 40 Nevada 37 New Hampshire 36 New Jersey 165 New Mexico 46 New York 450 North Carolina 178 North Dakota 27 Northern Mariana Islands 1 Ohio 288 Oklahoma 104 Oregon 76 Palau 1 Pennsylvania 345 Puerto Rico 156 Rhode Island 23 South Carolina 98 South Dakota 27 Tennessee 157 Texas 429 Utah 68 Vermont 20 Virgin Islands 2 Virginia 167 Washington 105 West Virginia 72 Wisconsin 94 Wyoming 10 Name: INSTNM, dtype: int64
The dataframe above shows the number of schools per state.
num_schools = schools.groupby('STATE')['INSTNM'].count()
# convert the series to dataframe
num_schools = num_schools.to_frame().reset_index()
#rename the column
num_schools = num_schools.rename(columns={"INSTNM": "COUNT"})
num_schools
| STATE | COUNT | |
|---|---|---|
| 0 | Alabama | 87 |
| 1 | Alaska | 9 |
| 2 | American Samoa | 1 |
| 3 | Arizona | 120 |
| 4 | Arkansas | 90 |
| 5 | California | 705 |
| 6 | Colorado | 94 |
| 7 | Connecticut | 78 |
| 8 | Delaware | 19 |
| 9 | District of Columbia | 26 |
| 10 | Federated States of Micronesia | 1 |
| 11 | Florida | 394 |
| 12 | Georgia | 174 |
| 13 | Guam | 3 |
| 14 | Hawaii | 23 |
| 15 | Idaho | 39 |
| 16 | Illinois | 253 |
| 17 | Indiana | 136 |
| 18 | Iowa | 77 |
| 19 | Kansas | 79 |
| 20 | Kentucky | 89 |
| 21 | Louisiana | 121 |
| 22 | Maine | 37 |
| 23 | Maryland | 84 |
| 24 | Massachusetts | 153 |
| 25 | Michigan | 187 |
| 26 | Minnesota | 112 |
| 27 | Mississippi | 59 |
| 28 | Missouri | 157 |
| 29 | Montana | 32 |
| 30 | Nebraska | 40 |
| 31 | Nevada | 37 |
| 32 | New Hampshire | 36 |
| 33 | New Jersey | 165 |
| 34 | New Mexico | 46 |
| 35 | New York | 450 |
| 36 | North Carolina | 178 |
| 37 | North Dakota | 27 |
| 38 | Northern Mariana Islands | 1 |
| 39 | Ohio | 288 |
| 40 | Oklahoma | 104 |
| 41 | Oregon | 76 |
| 42 | Palau | 1 |
| 43 | Pennsylvania | 345 |
| 44 | Puerto Rico | 156 |
| 45 | Rhode Island | 23 |
| 46 | South Carolina | 98 |
| 47 | South Dakota | 27 |
| 48 | Tennessee | 157 |
| 49 | Texas | 429 |
| 50 | Utah | 68 |
| 51 | Vermont | 20 |
| 52 | Virgin Islands | 2 |
| 53 | Virginia | 167 |
| 54 | Washington | 105 |
| 55 | West Virginia | 72 |
| 56 | Wisconsin | 94 |
| 57 | Wyoming | 10 |
num_schools.describe()
| COUNT | |
|---|---|
| count | 58.000000 |
| mean | 114.844828 |
| std | 131.155031 |
| min | 1.000000 |
| 25% | 28.250000 |
| 50% | 81.500000 |
| 75% | 155.250000 |
| max | 705.000000 |
num_schools.plot.bar(x = 'STATE', y = 'COUNT', figsize=(18,10))
<AxesSubplot:xlabel='STATE'>
There is median of 81 schools in the states. Atleast one school in each state. California has the highest number of schools (705).
2. The distribution of the overall completion rate:¶
- Provide choice of completion rate variable with a justification for that choice.
- Describe the distribution of that variable numerically and visually.
- What is the mean? Is the distribution skewed?
I selected C_100 and C_150 as the completion rates. The rational for this has been explained in the selection of variable section above.
schools
| INSTNM | CITY | STABBR | ADM_RATE | ADM_RATE_ALL | OPENADMP | STATE | CONTROL_STATUS | HIGHDEG_TYPE | ICLEVEL_TYPE | C_100 | C_150 | ADM | ADM_ALL | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Alabama A & M University | Normal | AL | 0.8965 | 0.8965 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.1052 | 0.2866 | Low-selectivity | Low-selectivity |
| 1 | University of Alabama at Birmingham | Birmingham | AL | 0.8060 | 0.8060 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.3816 | 0.6117 | Low-selectivity | Low-selectivity |
| 2 | Amridge University | Montgomery | AL | NaN | NaN | 1.0 | Alabama | Private, Nonprofit | Graduate degree | 4 Year | 0.2500 | 0.2500 | Open-admission | Open-admission |
| 3 | University of Alabama in Huntsville | Huntsville | AL | 0.7711 | 0.7711 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.3109 | 0.5714 | Low-selectivity | Low-selectivity |
| 4 | Alabama State University | Montgomery | AL | 0.9888 | 0.9888 | 2.0 | Alabama | Public | Graduate degree | 4 Year | 0.1462 | 0.3177 | Low-selectivity | Low-selectivity |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 6657 | Pennsylvania State University-Penn State Wilke… | Lehman | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6658 | Pennsylvania State University-Penn State York | York | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6659 | Pennsylvania State University-Penn State Great… | Malvern | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6660 | Pennsylvania State University-Penn State Harri… | Middletown | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
| 6661 | Pennsylvania State University-Penn State Brand… | Media | PA | NaN | 0.7827 | NaN | Pennsylvania | Public | Non-degree-granting | 4 Year | NaN | NaN | Open-admission | Low-selectivity |
6662 rows × 14 columns
com = schools[['C_100', 'C_150']]
com
| C_100 | C_150 | |
|---|---|---|
| 0 | 0.1052 | 0.2866 |
| 1 | 0.3816 | 0.6117 |
| 2 | 0.2500 | 0.2500 |
| 3 | 0.3109 | 0.5714 |
| 4 | 0.1462 | 0.3177 |
| … | … | … |
| 6657 | NaN | NaN |
| 6658 | NaN | NaN |
| 6659 | NaN | NaN |
| 6660 | NaN | NaN |
| 6661 | NaN | NaN |
6662 rows × 2 columns
com.describe()
| C_100 | C_150 | |
|---|---|---|
| count | 5187.000000 | 5450.000000 |
| mean | 0.373388 | 0.557012 |
| std | 0.270354 | 0.233730 |
| min | 0.000000 | 0.000000 |
| 25% | 0.148400 | 0.371500 |
| 50% | 0.328100 | 0.574500 |
| 75% | 0.567700 | 0.733300 |
| max | 1.000000 | 1.000000 |
plt.hist(com['C_100'], bins = 20)
(array([575., 330., 405., 375., 360., 376., 327., 272., 258., 249., 273.,
232., 188., 190., 163., 162., 136., 112., 79., 125.]),
array([0. , 0.05, 0.1 , 0.15, 0.2 , 0.25, 0.3 , 0.35, 0.4 , 0.45, 0.5 ,
0.55, 0.6 , 0.65, 0.7 , 0.75, 0.8 , 0.85, 0.9 , 0.95, 1. ]),
<BarContainer object of 20 artists>)
plt.hist(com['C_150'], bins = 20)
(array([ 69., 39., 85., 171., 236., 299., 331., 286., 312., 297., 419.,
391., 410., 432., 438., 340., 301., 213., 178., 203.]),
array([0. , 0.05, 0.1 , 0.15, 0.2 , 0.25, 0.3 , 0.35, 0.4 , 0.45, 0.5 ,
0.55, 0.6 , 0.65, 0.7 , 0.75, 0.8 , 0.85, 0.9 , 0.95, 1. ]),
<BarContainer object of 20 artists>)
sns.set(style="darkgrid")
sns.boxplot(data=com.loc[:, ['C_100', 'C_150']])
plt.show()
More students completed in 150% of expected time of completion than 100%. The mean completion rate is 0.37 and 0.56 for C_100 and C_150 respectively. C_100 is slightly left skewed while C_150 is normally distributed.
3. The distribution of the admission rate, both numerically and graphically¶
After describing the distribution of the continuous admission rate, compute the admissions category (open, low-selectivity, or high-selectivity). Do not hard-code the median — compute the median, and use the computed value (stored in a Python variable) to bucketize the admission rates. Show the distribution of admissions category (how many schools are in each category?).
adm = schools[['ADM_RATE', 'ADM']]
adm.describe()
| ADM_RATE | |
|---|---|
| count | 1960.000000 |
| mean | 0.711634 |
| std | 0.212352 |
| min | 0.000000 |
| 25% | 0.595550 |
| 50% | 0.751800 |
| 75% | 0.874225 |
| max | 1.000000 |
plt.hist(adm['ADM_RATE'], bins = 20)
(array([ 3., 20., 16., 19., 23., 20., 37., 57., 45., 61., 88.,
114., 128., 156., 181., 227., 201., 159., 185., 220.]),
array([0. , 0.05, 0.1 , 0.15, 0.2 , 0.25, 0.3 , 0.35, 0.4 , 0.45, 0.5 ,
0.55, 0.6 , 0.65, 0.7 , 0.75, 0.8 , 0.85, 0.9 , 0.95, 1. ]),
<BarContainer object of 20 artists>)
The mean admission rate is 0.71 and it is right skewed. I have bucketized the admnission rate in the data data section
plt.hist(adm['ADM'])
(array([ 979., 0., 0., 0., 0., 4704., 0., 0., 0.,
979.]),
array([0. , 0.2, 0.4, 0.6, 0.8, 1. , 1.2, 1.4, 1.6, 1.8, 2. ]),
<BarContainer object of 10 artists>)
About 1000 schools are in low-selectivity and high-selectivity category and 5000 are in open-admission category
4. The break down (sometimes called a disaggregation) of completion rate by race, by the school characteristics described in “Question”, and by one additional school characteristic you select.¶
Give a justification for your choice of additional characteristic — why do you think it might be interesting?
You need to show these breakdowns both numerically and graphically. Box plots are useful for this, as are bar charts.
# read the csv file and select the completion rates by race
rate_race_4 = pd.read_csv('../../Data/Most-Recent-Cohorts-Institution_04262022/Most-Recent-Cohorts-Institution.csv',
usecols= ['INSTNM' ,'C150_4_WHITE', 'C150_4_BLACK', 'C150_4_HISP', 'C150_4_ASIAN', 'C150_4_AIAN', 'C150_4_NHPI', 'C150_4_2MOR', 'C150_4_NRA', 'C150_4_UNKN'])
# read the csv file and select the completion rates by race
rate_race_L4 = pd.read_csv('../../Data/Most-Recent-Cohorts-Institution_04262022/Most-Recent-Cohorts-Institution.csv',
usecols= ['INSTNM', 'C150_L4_WHITE', 'C150_L4_BLACK', 'C150_L4_HISP', 'C150_L4_ASIAN', 'C150_L4_AIAN', 'C150_L4_NHPI', 'C150_L4_2MOR', 'C150_L4_NRA', 'C150_L4_UNKN'])
rate_race_4.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 6662 entries, 0 to 6661 Data columns (total 10 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 INSTNM 6662 non-null object 1 C150_4_WHITE 2143 non-null float64 2 C150_4_BLACK 1963 non-null float64 3 C150_4_HISP 2027 non-null float64 4 C150_4_ASIAN 1738 non-null float64 5 C150_4_AIAN 1346 non-null float64 6 C150_4_NHPI 904 non-null float64 7 C150_4_2MOR 1714 non-null float64 8 C150_4_NRA 1564 non-null float64 9 C150_4_UNKN 1661 non-null float64 dtypes: float64(9), object(1) memory usage: 520.6+ KB
rate_race_L4.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 6662 entries, 0 to 6661 Data columns (total 10 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 INSTNM 6662 non-null object 1 C150_L4_WHITE 1516 non-null float64 2 C150_L4_BLACK 1415 non-null float64 3 C150_L4_HISP 1416 non-null float64 4 C150_L4_ASIAN 1121 non-null float64 5 C150_L4_AIAN 939 non-null float64 6 C150_L4_NHPI 599 non-null float64 7 C150_L4_2MOR 1187 non-null float64 8 C150_L4_NRA 595 non-null float64 9 C150_L4_UNKN 1002 non-null float64 dtypes: float64(9), object(1) memory usage: 520.6+ KB
From the two info dataframes above, we see that there are missing values for the completion rate by race records. For example, of the 6k records, there are 2143 records for completion rates of white race at 4 year (C150_4_WHITE) and 1516 records for C150_L4_WHITE. Let’s combine these values since we have earlier confirmed that there is no instutuition that appear in both columns. For this combination, I write a for loop that iterates over each race column and perform the combination. The combined race is stored in a varible determined by the last string of the race column. For example, ‘C150_4_WHITE’ and ‘C150_L4_WHITE’ are combined to ‘WHITE’. Then I dropped the columns that appropriate columns after combining. This is done in the next code cells
for i in range(rate_race_4.shape[1]):
if i > 0:
#print(rate_race_4.columns[i])
rate_race_4[rate_race_4.columns[i].split('_')[2]] = rate_race_4[rate_race_4.columns[i]].combine_first(rate_race_L4[rate_race_L4.columns[i]])
rate_race = rate_race_4.drop(['C150_4_WHITE', 'C150_4_BLACK', 'C150_4_HISP', 'C150_4_ASIAN', 'C150_4_AIAN', 'C150_4_NHPI', 'C150_4_2MOR', 'C150_4_NRA', 'C150_4_UNKN'], axis = 1)
rate_race.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 6662 entries, 0 to 6661 Data columns (total 10 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 INSTNM 6662 non-null object 1 WHITE 3659 non-null float64 2 BLACK 3378 non-null float64 3 HISP 3443 non-null float64 4 ASIAN 2859 non-null float64 5 AIAN 2285 non-null float64 6 NHPI 1503 non-null float64 7 2MOR 2901 non-null float64 8 NRA 2159 non-null float64 9 UNKN 2663 non-null float64 dtypes: float64(9), object(1) memory usage: 520.6+ KB
As shown in the info dataframe above, white now has 3359 record which is the combination of records in ‘C150_4_WHITE’ and ‘C150_L4_WHITE’
rate_race.describe()
| WHITE | BLACK | HISP | ASIAN | AIAN | NHPI | 2MOR | NRA | UNKN | |
|---|---|---|---|---|---|---|---|---|---|
| count | 3659.000000 | 3378.000000 | 3443.000000 | 2859.000000 | 2285.000000 | 1503.000000 | 2901.000000 | 2159.000000 | 2663.000000 |
| mean | 0.526352 | 0.383435 | 0.469504 | 0.555214 | 0.394889 | 0.424855 | 0.444463 | 0.523566 | 0.465052 |
| std | 0.233955 | 0.267019 | 0.265012 | 0.315253 | 0.370270 | 0.411903 | 0.283066 | 0.303001 | 0.312280 |
| min | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 0.354450 | 0.171175 | 0.266700 | 0.333300 | 0.000000 | 0.000000 | 0.230800 | 0.330100 | 0.222200 |
| 50% | 0.534000 | 0.333300 | 0.453800 | 0.571400 | 0.333300 | 0.333300 | 0.428600 | 0.529400 | 0.464300 |
| 75% | 0.692700 | 0.558100 | 0.666700 | 0.800000 | 0.666700 | 1.000000 | 0.641100 | 0.750000 | 0.688700 |
| max | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 | 1.000000 |
Let’s plot the histogram for the completion rate and the box plot based on race
rate_race.plot.hist(subplots=True, layout = (2, 5), figsize=(18,12))
plt.tight_layout()
plt.show()
rate_race.boxplot(column = ['WHITE', 'BLACK', 'HISP', 'ASIAN', 'AIAN', 'NHPI', '2MOR', 'NRA', 'UNKN'], figsize=(18,12))
plt.show()
The mean completion rate is lowest for BLACK and highest for ASIAN. For completion rates by selectivity. I have already bin the admission rates into three class in the schools dataframe
rate_selectivity = schools[['INSTNM', 'STATE', 'C_100', 'C_150', 'ADM']]
rate_selectivity
| INSTNM | STATE | C_100 | C_150 | ADM | |
|---|---|---|---|---|---|
| 0 | Alabama A & M University | Alabama | 0.1052 | 0.2866 | Low-selectivity |
| 1 | University of Alabama at Birmingham | Alabama | 0.3816 | 0.6117 | Low-selectivity |
| 2 | Amridge University | Alabama | 0.2500 | 0.2500 | Open-admission |
| 3 | University of Alabama in Huntsville | Alabama | 0.3109 | 0.5714 | Low-selectivity |
| 4 | Alabama State University | Alabama | 0.1462 | 0.3177 | Low-selectivity |
| … | … | … | … | … | … |
| 6657 | Pennsylvania State University-Penn State Wilke… | Pennsylvania | NaN | NaN | Open-admission |
| 6658 | Pennsylvania State University-Penn State York | Pennsylvania | NaN | NaN | Open-admission |
| 6659 | Pennsylvania State University-Penn State Great… | Pennsylvania | NaN | NaN | Open-admission |
| 6660 | Pennsylvania State University-Penn State Harri… | Pennsylvania | NaN | NaN | Open-admission |
| 6661 | Pennsylvania State University-Penn State Brand… | Pennsylvania | NaN | NaN | Open-admission |
6662 rows × 5 columns
Let’s group by selectivity classes and compute the completion stats with the group
rate_selectivity.groupby('ADM')['C_100'].agg(['mean', 'count'])
| mean | count | |
|---|---|---|
| ADM | ||
| High-selectivity | 0.469671 | 916 |
| Low-selectivity | 0.398665 | 923 |
| Open-admission | 0.340077 | 3348 |
# set a grey background (use sns.set_theme() if seaborn version 0.11.0 or above)
sns.set(style="darkgrid")
sns.boxplot(x= rate_selectivity["ADM"], y=rate_selectivity["C_100"])
plt.show()
rate_selectivity.groupby('ADM')['C_150'].agg(['mean', 'count'])
| mean | count | |
|---|---|---|
| ADM | ||
| High-selectivity | 0.596320 | 947 |
| Low-selectivity | 0.551019 | 940 |
| Open-admission | 0.548145 | 3563 |
sns.set(style="darkgrid")
sns.boxplot(x= rate_selectivity["ADM"], y=rate_selectivity["C_150"])
plt.show()
Open admission schools have low median completion rate than low selectivity and high-selectivity. High-selectivity has the highest completion rate.
For completion rate by CONTROL
rate_control = schools[['INSTNM', 'STATE', 'C_100', 'C_150', 'CONTROL_STATUS']]
rate_control
| INSTNM | STATE | C_100 | C_150 | CONTROL_STATUS | |
|---|---|---|---|---|---|
| 0 | Alabama A & M University | Alabama | 0.1052 | 0.2866 | Public |
| 1 | University of Alabama at Birmingham | Alabama | 0.3816 | 0.6117 | Public |
| 2 | Amridge University | Alabama | 0.2500 | 0.2500 | Private, Nonprofit |
| 3 | University of Alabama in Huntsville | Alabama | 0.3109 | 0.5714 | Public |
| 4 | Alabama State University | Alabama | 0.1462 | 0.3177 | Public |
| … | … | … | … | … | … |
| 6657 | Pennsylvania State University-Penn State Wilke… | Pennsylvania | NaN | NaN | Public |
| 6658 | Pennsylvania State University-Penn State York | Pennsylvania | NaN | NaN | Public |
| 6659 | Pennsylvania State University-Penn State Great… | Pennsylvania | NaN | NaN | Public |
| 6660 | Pennsylvania State University-Penn State Harri… | Pennsylvania | NaN | NaN | Public |
| 6661 | Pennsylvania State University-Penn State Brand… | Pennsylvania | NaN | NaN | Public |
6662 rows × 5 columns
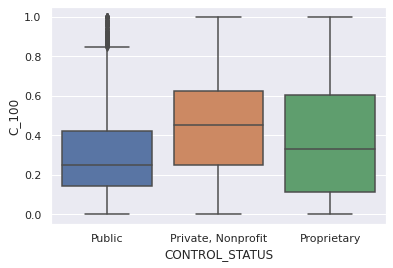
rate_control.groupby('CONTROL_STATUS')['C_100'].agg(['mean', 'count'])
| mean | count | |
|---|---|---|
| CONTROL_STATUS | ||
| Private, Nonprofit | 0.437661 | 1394 |
| Proprietary | 0.376065 | 2063 |
| Public | 0.318407 | 1730 |
# set a grey background (use sns.set_theme() if seaborn version 0.11.0 or above)
sns.set(style="darkgrid")
sns.boxplot(x= rate_control["CONTROL_STATUS"], y= rate_control["C_100"])
plt.show()
The boxplot shows that private instituitions has higher median completion rate than public instituition
# set a grey background (use sns.set_theme() if seaborn version 0.11.0 or above)
sns.set(style="darkgrid")
sns.boxplot(x= rate_control["CONTROL_STATUS"], y= rate_control["C_150"])
<AxesSubplot:xlabel='CONTROL_STATUS', ylabel='C_150'>
The addition school characteristics that I choose is the DEGREE TYPE. The rational behind this choise is that the higher the degree, the more challenging it becomes to complete
rate_highdegree = schools[['INSTNM', 'STATE', 'C_100', 'C_150', 'HIGHDEG_TYPE']]
rate_icleveltype = schools[['INSTNM', 'STATE', 'C_100', 'C_150', 'ICLEVEL_TYPE']]
# set a grey background (use sns.set_theme() if seaborn version 0.11.0 or above)
sns.set(style="darkgrid")
sns.boxplot(x= rate_highdegree["HIGHDEG_TYPE"], y= rate_highdegree["C_100"])
plt.show()
# set a grey background (use sns.set_theme() if seaborn version 0.11.0 or above)
sns.set(style="darkgrid")
sns.boxplot(x= rate_icleveltype["ICLEVEL_TYPE"], y= rate_icleveltype["C_100"])
plt.show()
# set a grey background (use sns.set_theme() if seaborn version 0.11.0 or above)
sns.set(style="darkgrid")
sns.boxplot(x= rate_icleveltype["ICLEVEL_TYPE"], y= rate_icleveltype["C_150"])
plt.show()
Based on the boxplot above, less than 2 years degree has higher completion rates than 4 years degress